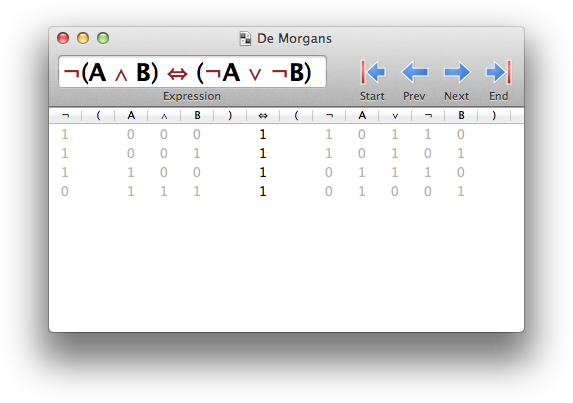
Examples
De Morgan's Law (Wikipedia)
Satisfiability (3-CNF)
- (A | B | C) & (A | ~B | ~C) & (~A | ~B | C)
- (A | ~B | ~C) & (~A | ~B | ~C) & (A | B | ~C) & (A | ~B | C)
Full Adder
Usage
Operators in order of evaluation. All identifiers must be uppercase.
| Symbol | Meaning |
|---|---|
| 1 | Always true. |
| 0 | Always false. |
| ~ | Takes one postfix argument. True if the arugment is false, and false if the argument is true. |
| + | Takes two arguments. True if exactly one of the arguments is true, false otherwise. |
| & | Takes two arguments. True if both of the arguments are true, false otherwise. |
| | | Takes two arguments. True if either of the are true, false otherwise. |
| -> | Takes two arguments. False, if and only if the first term is true, and the second term is false. |
| <-> | Takes two arguments. True if both arguments are the same, false otherwise. |
| / | Splits an expression, so that multiple expressions can be entered. |
Still Struggling?
Strugging with truth tables? I made this app just for you - quickly generate truth tables from any boolean logic statement - it also includes an interactive tutor that teaches you how to solve truth tables step-by-step! Download Now!
comments powered by Disqus